PROTOMODALISM 3

by Arco-X

The idea which sprang unexpectedly into my head, and kick-started my protomodal project was this:

The tonic is a fixed datum, and the mode can be represented by a six digit quaternary (Base 4) number, where each digit represents one of the intervals between the seven tones.  The intervals can be a minor 2^nd (e.g. B to C), a major 2^nd (C to D), an aumented 2^nd (C to D♯), or a doubly augmented 2^nd (G♭ to A♯).  These four possible intervals are represented by the numbers 0, 1, 2 and 3 respectively.  My specific definition of a heptatonic mode is that it contains all of the tones A through G, one of which is the tonic, and each of which can occur in one of the three variants sharp, flat or natural. 

So the Major (or Ionian) mode, in which the intervals are maj. 2^nd,  maj. 2^nd, min. 2^nd, maj. 2^nd, maj. 2^nd, maj. 2^nd can be uniquely represented by 110111 which, converted to decimal, is 1,301.  This system gives us a series of numbers from 000000 (decimal 0) to 333333 (4,095), contained within which are all the possible heptatonic modes.  Not all of these numbers will represent valid modes because the 6 digits, plus the unused seventh digit representing the interval between the leading tone and the tonic, have to add up to 5 to complete the octave from tonic to tonic.  Think about it;  the 5 equals the semitones unused in the mode out of the octave’s twelve.  So the series includes a number of combinations which either fail to extend to a complete octave or stretch beyond it.  333333, for instance, extends over 2 octaves.  I programmed an Excel spreadsheet to do the calculations which revealed that the series 0 to 4,095 includes 399 possible heptatonic modes, and precisely which tones each is composed of.

Some of the modes uniquely occur in only one key, and some pretty odd keys at that, like B♯ and F♭.  The lowest number which gives a valid mode is 000011 (5) which gives us B♯ C♯ D E♭ F♭ G♭ A;  while the highest 311000 (3392) gives F♭ G♯ A♯ B♯ C♯ D E♭.  Transposing some these unusual modes into other keys may require the use of double, treble and even quadruple accidentals so is probably better avoided. 

At this stage of my research it was beginning to feel a bit abstruse, like understanding subatomic particles or the square root of -1, but it was getting very exciting.

The Excel spreadsheet was substantially expanded into an essential tool for the protomodal composer:

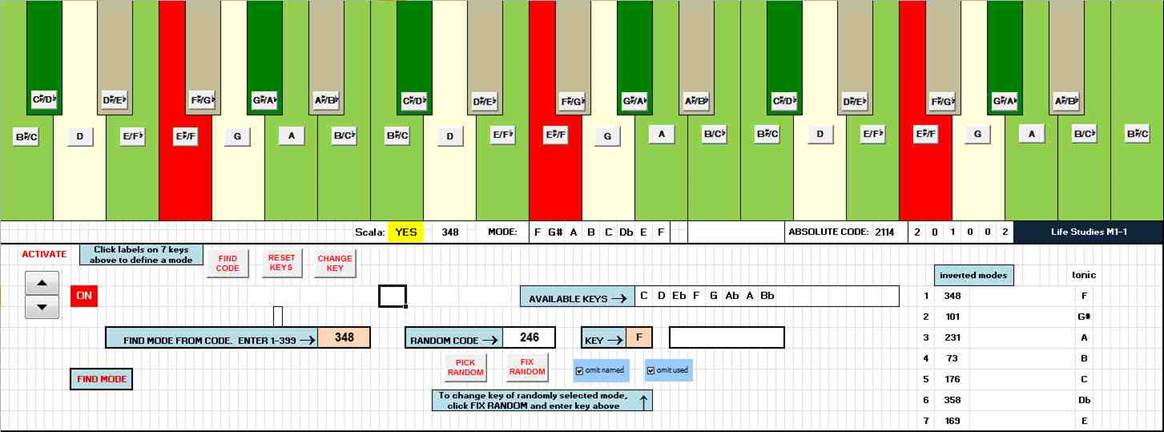
The modes are rationalized in an indexed list from 1 to 399.  Entering any of these numbers will display the associated mode, graphically on the keyboard and as a list.  The display also shows which keys are available without the use of multiple accidentals.  Conversely, entering a mode by clicking seven notes on the keyboard will show the index number.  Most important of all for my composing method, a random mode can be generated by chance and the selection filtered, if required, to omit the existing named modes or those which I have already used in compositions.  A separate page shows which nameable chords are available in the given mode:

The spreadsheet has other clever functions which I shall describe if and when their relevance becomes apparent in my continuing discourse.  It’s a neat little tool, and the protomodal method has given me a great creative boost.

HOME SCRITTO INDEX